Question

Please help! Vectors and angles

A ship is sailing through the water in the English Channel with a velocity of 22 knots along a bearing of 157° (knots being a unit used to measure the speed of aircrafts and boats). The current has a velocity of 5 knots along a bearing of 213°. Find the resultant velocity and direction of the ship. (Remember that bearing is measured clockwise from the north axis).
1) 25 knots at 166.5 degree
2) 27 knots at 350 degree
3) 166.5 knots at 25 degree
4) 350 knots at 27 degree

Answer 1

The answer is A. I am doing Pearson Connexus and had this same question. It showed A was the correct answer to this question.

Answer 2

We have been given that a ship is sailing through the water in the English Channel with a velocity of 22 knots along a bearing of 157°.

Further we have been given that current has a velocity of 5 knots along a bearing of 213°.

Therefore, angle between the direction of ship and direction of current will be

`\theta = 213 - 157 = 56^(0)`

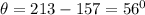
We can find the magnitude of resultant by using parallelogram law of vectors.

`R=\sqrt{P^(2)+Q^(2)+2PQcos(\theta)}`

Upon substituting
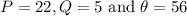`P=22, Q = 5 \text{ and }\theta = 56` in this formula, we get

`R=\sqrt{22^(2)+5^(2)+2\cdot 22\cdot 5cos(56)}\\ R=√(484+25+220\cdot0.55919)\\ R=√(632.0224)\\ R=25.14 \text{ knots}`

Therefore, resultant velocity of the ship is 25.14 knots.

We find the angle of resultant from P, that direction of ship using the formula

`\alpha = arctan((Qsin(\theta))/(P+Qcos(\theta)))`

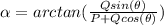
Upon substituting the values, we get

`\alpha = arctan((5sin(56))/(22+5cos(56)))\\ \alpha = arctan((4.14518)/(24.79596))\\ \alpha = arctan(0.16717)\\ \alpha = 9.49^(0)`

Therefore, bearing of the resultant is
`157+9.49 = 166.49^(0)`

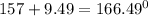
Hence, option (A) is the correct choice!