Question

Leanne is picking out some movies to rent, and she is primarily interested in children's movies and comedies. She has narrowed down her selections to 18 children's movies and 7 comedies. Step 2 of 2 : How many different combinations of 3 movies can she rent if she wants at least one comedy

Answer 1

If she wants at least one comedy, there are 1484 different combinations.

Explanation:

The order in which she wants to pick the movies is not important. So, we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question:

She wants combinations of 3 movies, with at least one comedy. The easiest way to find this is finding the total number of combinations of 3 movies, from the set of 25(18 children's and 7 comedies), and subtract by the total number without comedies(which is 3 from a set of 25). So

Total:

3 from a set of 25.

`C_(25,3) = (25!)/(3!(25-3)!) = 2300`

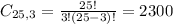
Without comedies:

3 from a set of 18.

`C_(18,3) = (18!)/(3!(18-3)!) = 816`

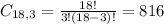
At least one comedy:

`2300 - 816 = 1484`

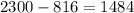
If she wants at least one comedy, there are 1484 different combinations.