Question

d. Calculate the initial reaction rate that would be seen in a solution in which [BF3] is 5.0 x10 -1M and [NH3] is 2.0 x10 -2 M

Answer 1

`r=0.0341(M)/(s)`

Step-by-step explanation:

Hello!

In this case, considering the given table, we are able to represent the symbolic rate law as shown below:

`r=k[BF_3]^m[NH_3]^n`

Thus, by using the following steps, we can find both m (BF3 order of reaction) and n (BF3 order of reaction):

- Experiment 1 and 2 for the calculation of n:

`(r_1)/(r_2)=(k[BF_3]_1^m[NH_3]_1^n)/(k[BF_3]_2^m[NH_3]_2^n)`

So we plug in to obtain:

`(0.2130)/(0.1065)=(k*0.250^m*0.250^n)/(k*0.250^m*0.125^n)\\\\2=(0.250^n)/(0.125^n)\\\\2=2^n\\\\log(2)=n*log(2)\\\\n=1`

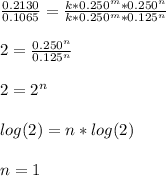
So the order of reaction with respect to NH3 is 1.

- Experiment 3 and 4 for the calculation of m

`(r_3)/(r_4)=(k[BF_3]_3^m[NH_3]_3^n)/(k[BF_3]_4^m[NH_3]_4^n)`

So we plug in to obtain:

`(0.0682)/(0.1193)=(k*0.200^m*0.100^n)/(k*0.350^m*0.100^n)\\\\0.57=0.57^m\\\\log(0.57)=m*log(0.57)\\\\m=1`

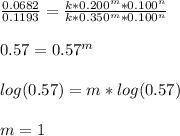
So the order of reaction with respect to BF3 is also 1.

Now, we can compute the rate constant by solving for it on any of the experiments there, say experiment 1:

`k=(r_1)/([BF_3][NH_3]) =(0.2130M/s)/(0.250M*0.250M)\\\\k=3.41M^(-1)s^(-1)`

Thus, the initial reaction rate for the 0.50M BF3 and 0.020M NH3 is:

`r=3.41M^(-1)s^(-1)*0.50M*0.020M\\\\r=0.0341(M)/(s)`

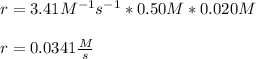
Best regards!