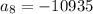Question

Find the 8th term of the geometric sequence 5, -15, 45, ...5,−15,45,...​

Answer 1

The 8th term of the geometric sequence 5, -15, 45, ... is:

`a_8=-10935`

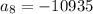
Explanation:

Given the geometric sequence

5, -15, 45, ...

The first element of the geometric sequence is

`a_1=5`

A geometric sequence has a constant ratio 'r' and is defined by

`a_n=a_1\cdot r^(n-1)`

computing the ratios of all the adjacent terms

`(-15)/(5)=-3,\:\quad (45)/(-15)=-3`

The ratio between all the adjacent terms is the same and equal to

`r=-3`

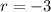
substituting
`a_1=5`, and
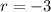`r=-3` in the nth term

`a_n=a_1\cdot r^(n-1)`

`a_n=5\left(-3\right)^(n-1)`

Determining the 8th term:

We have already got the nth term

`a_n=5\left(-3\right)^(n-1)`

substituting n = 8 to determine the 8th term

`a_n=5\left(-3\right)^(n-1)`

`a_8=5\left(-3\right)^(8-1)`

`a_8=5\left(-3^7\right)`

`a_8=-5\cdot \:3^7`

`a_8=-5\cdot \:2187`

`a_8=-10935`

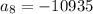
Therefore, the 8th term of the geometric sequence 5, -15, 45, ... is:

`a_8=-10935`