Greetings!
The equation of a line in slope-intercept form is:
y = mx + b
m is the slope
b is the y- intercept
What we need to do is to re-arrange 2x - 9y - 18 = 0. We wanna make it looks like y = mx + b
So, the equation is:
2x - 9y - 18 = 0
Subtract 2x - 18 from both sides
→ -9y = -2x + 18
Since we want y, we need to divide both sides by -9
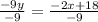
Thus,
y = 2/9 x - 2 which is in the slope intercept form
Slope m = 2/9 and the y-intercept is = - 2
Given a line with slope m then the slope of a line perpendicular is:
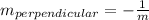
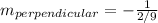
= - 9/2
Thus,
The equation of the function is:

Let me know if you have questions about the answer. As always, it is my pleasure to help students like you!