Question

Does this sample support a claim that more than 10% of job applicants in California test positive for drug use

Answer 1

Following are the solution to this question:

Explanation:

Please find the complete question in the attached file.

Let p become a screen positive for substance use throughout California

To test
`H_0 : p = 0.1_(against) \ H_0:p>0.1`

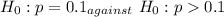
In California,
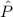`\hat{P}` is a good test for medication and n seems to be the random sample.

The stats of the examination are given

`\to z=\frac{\hat{p} -0.1}{\sqrt{(0.1 * 0.9)/(n) }}_(\ that \ is \ under H_o \ follows \ a \ normal \ distribution).`

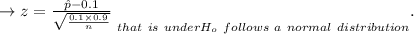
They reject
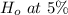`H_o \ at \ 5\%` if it's relevant:

`\to |Z_(obs) |> Z_(0.05)\\\\Here\\\\ \to \hat{p} = (145)/(1200) = 0.121 \\\\ \to n = 1200\\\\ \to z_(obs) = 2.42487\\\\ \to Z_(0.05) = 1.64485`

`\to z_(obs) = 2.42487 > z_(0.05)= 1.64485`

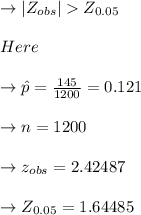
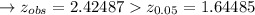
We, therefore, refuse
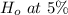`H_o \ at \ 5\%` level and we can infer that such a test supports an argument which Upwards of 10% of California jobseekers screen positive for use of medicines.