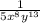Question

Which expression is equivalent to 3x^-6y^-3/15x^2y^10

Answer 1

`(3x^(-6)y^(-3))/(15x^2y^(10))=(1)/(5)x^(-6-2)y^(-3-10)=(1)/(5)x^(-8)y^(-13)=(x^(-8)y^(-13))/(5)=(1)/(5x^8y^(13))\\\\Used:\\\\(a^n)/(a^m)=a^(n-m)\\\\a^(-n)=(1)/(a^n)`

Answer 2

`(1)/(5x^(8)y^(13))`

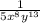
Explanation:

`(3x^(-6)y^(-3))/(15x^2y^(10))`

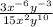
To find out equivalent expression we need to simplify it

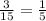`(3)/(15) =(1)/(5)` divided 3 on both sides

To simplify variables , use exponential property

`(a^m)/(a^n) =a^(m-n)`

`(x^(-6))/(x^2) =x^(-6-2)=x^(-8)`

`(y^(-3))/(y^(10)) =y^(-3-10)=x^(-13)`

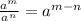
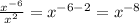
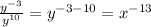
Our expression becomes

`(x^(-8)y^(-13))/(5)`

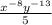
To remove negative exponent we move the variable with exponent to the denominator

`(1)/(5x^(8)y^(13))`