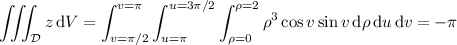Question

2) Use spherical coordinates to find the integral of f(x,y,z) = z over x^2 + y^2 + z^2 < 4 and x,y,z < 0

Answer 1

1. Denote by
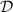
`\mathcal D` the region bounded by the cylinder
`x^2+y^2=9` and the planes
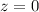
`z=0` and
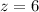
`z=6`. Converting to cylindrical coordinates involves setting



`\begin{cases}x=r\cos u\\y=r\sin u\\z=v\end{cases}`


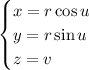
and
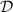
`\mathcal D` is obtained by varying the parameters over
`0\le r\le3`,
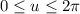
`0\le u\le2\pi`, and
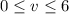
`0\le v\le6`. The volume element is



`\mathrm dV=\mathrm dx\,\mathrm dy\,\mathrm dz=r\,\mathrm dr\,\mathrm du\,\mathrm dv`

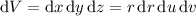
so the integral becomes


`\displaystyle\iiint_(\mathcal D)xz\,\mathrm dV=\int_(v=0)^(v=6)\int_(u=0)^(u=2\pi)\int_(r=0)^(r=3)r^2v\cos u\,\mathrm dr\,\mathrm du\,\mathrm dv=0`

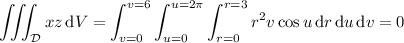
2. Now let
`\mathcal D` denote the region bounded by the sphere
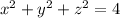
`x^2+y^2+z^2=4` and the coordinate planes in the octant in which each coordinate of the point
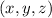
`(x,y,z)` is negative.

Converting to spherical coordinates, we set


`\begin{cases}x=\rho\cos u\sin v\\y=\rho\sin u\sin v\\z=\rho\cos v\end{cases}`

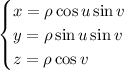
where we obtain
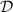
`\mathcal D` by varying over
`0\le\rho\le2`,
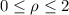
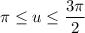
`\pi\le u\le\frac{3\pi}2`, and
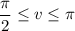
`\frac\pi2\le v\le\pi`. The volume element is now


`\mathrm dV=\rho^2\sin v\,\mathrm d\rho\,\mathrm du\,\mathrm dv`

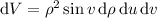
so the integral becomes


`\displaystyle\iiint_(\mathcal D)z\,\mathrm dV=\int_(v=\pi/2)^(v=\pi)\int_(u=\pi)^(u=3\pi/2)\int_(\rho=0)^(\rho=2)\rho^3\cos v\sin v\,\mathrm d\rho\,\mathrm du\,\mathrm dv=-\pi`