Explanation :
It is given that,
Mass of the rock, m = 20 kg
Initially the rock is at rest, u = 0
Final velocity of the rock is, v = 90 m/s
Gravitational potential energy is given by :
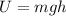 ............(1)
............(1)
h is the height.
Using third equation of motion :
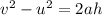
or
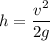
Put the value of h in equation (1)
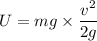
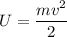
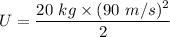
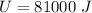
or
U = 81 kJ
Hence, this is the required solution.