Question

A 20.0-kg rock is dropped and hits the ground at a speed of 90.0 m/s. Calculate the rock’s gravitational potential energy before it was dropped. (Ignore the effects of friction.)

Answer 1

Answer:

GPE=81000J or 81kJ

Step-by-step explanation

Potential Energy = mgh = 20 x 9.8 x ?

To find H use one of the equation of motion

= [(90)^2 - 0 ] / 2(9.8)

Potential Energy = mgh = 20 x 9.8 x 8100 /2(9.8) = 81000 J

Answer 2

Explanation :

It is given that,

Mass of the rock, m = 20 kg

Initially the rock is at rest, u = 0

Final velocity of the rock is, v = 90 m/s

Gravitational potential energy is given by :

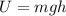`U=mgh`............(1)

h is the height.

Using third equation of motion :

`v^2-u^2=2ah`

or

`h=(v^2)/(2g)`

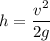
Put the value of h in equation (1)

`U=mg* (v^2)/(2g)`

`U=(mv^2)/(2)`

`U=(20\ kg* (90\ m/s)^2)/(2)`

`U=81000\ J`

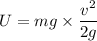
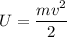
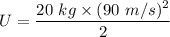
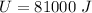
or

U = 81 kJ

Hence, this is the required solution.