Question

In ΔABC, ∡A is a right angle, and m∡B = 45°. What is the length of BC? If the answer is not an integer, leave it in simplest radical form. The diagram is not drawn to scale.

Answer 1

BC² = 11² + 11²

BC² = 121 + 121

BC² = 242

BC = √242

BC = 11√2

Answer: 11√2

Answer 2

The length of BC is 11√2 ft.

Explanation:

Given,

A right angled triangle ABC,

In which,

AC = 11 ft ( By diagram ),

∠A = 90°,

∠B = 45°,

By the law of sine,

`(sin B)/(AC)=(sin A)/(BC)`

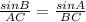
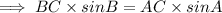`\implies BC* sin B = AC* sin A` ( By cross multiplication )

`\implies BC = (AC* sin A)/(sin B)`

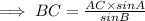
By substituting the values,

`BC=(11* sin 90^(\circ))/(sin 45^(\circ))`

`=(11)/((1)/(√(2)))`

`=11√(2)`

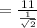
Hence, the length of BC is 11√2 ft.