Question 1) Vertex of the Parabola.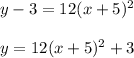
The vertex of the general parabolic equation:
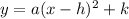
lies at (h,k)
Comparing the given equation to general equation, we can write:
h = - 5
k = 3
So, the vertex of the given parabola will be (-5, 3)Question 2) Equation of DirectrixThe correct equation of the parabola is:
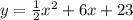
First we need to convert the equation to standard form as shown below:
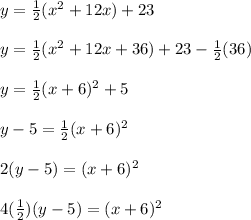
The directrix of the general parabola of the form:

is
y = k - pComparing equation of given parabola with general parabolic equation, we can write:
p =1/2
k = 5
So, equation of directirx will be:
y = 5 - 1/2 = 4.5So, option B gives the correct answer.Question 3) Focus of the parabolaThe correct equation of the parabola is:

Comparing this equation to the general parabolic equation, we can write:
p=8
h =1
k = 2
The focus of the parabola will be at
(h+p,k) = (9,2)So the focus of the parabola is at (9,2)
Thus, option D gives the correct answer.