Question

The probability of hitting a target is 1/8. What is the probability of hitting the target exactly twice in five tries

Answer 1

`P(X=2) = 0.1047`

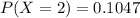
Explanation:

Represent the probability of hitting the target with H.

So:

`H = (1)/(8)`

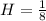
Represent the probability of not hitting the target with T.

So:

`T = 1 - H`

`T =1 - (1)/(8)`

`T =(7)/(8)`

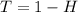
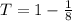
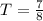
Required

Probability of exactly 2 hits in 5 tries

This probability is a binomial probability and will be calculated using:

`P(X=x) = ^nC_x H^xT^(n-x)`

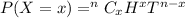
In this case:

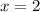`x = 2` i.e 2 hits

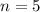`n = 5` i.e. 5 attempts

So, we have:

`P(X=2) = ^5C_2 H^2T^(5-2)`

`P(X=2) = ^5C_2 H^2T^3`

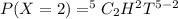
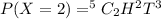
Apply combination formula:

`P(X=2) = (5!)/((5-2)!2!) H^2T^3`

`P(X=2) = (5!)/(3!2!) H^2T^3`

`P(X=2) = (5*4*3!)/(3!2*1) H^2T^3`

`P(X=2) = (5*4)/(2) H^2T^3`

`P(X=2) = 10* H^2T^3`

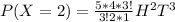
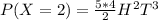
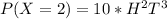
Substitute values for H and T

`P(X=2) = 10* ((1)/(8))^2((7)/(8))^3`

`P(X=2) = 10* (1)/(64)*(343)/(512)`

`P(X=2) = (3430)/(32768)`

`P(X=2) = 0.1047`

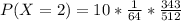
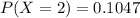
Hence, the probability of 2 hits in 5 tries is 0.1047