Question

Which of these expressions is equal to cos x?

Oa) sin(x - 45°)
Ob) sin x
c) sin (45° - x)
d) sin (90° - x)

Answer 1

`\sin \left(90^(\circ \:)-x\right)=\cos \left(x\right)`

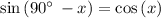
Hence, option D is correct.

Explanation:

Given the expression

`sin\:\left(90^(\circ )\:-\:x\right)`

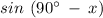
Using the angle difference identity

`\sin \left(s-t\right)=\sin \left(s\right)\cos \left(t\right)-\cos \left(s\right)\sin \left(t\right)`

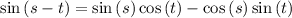
so the expression becomes

`sin\:\left(90^(\circ )\:-\:x\right)=\sin \:\left(90^(\circ \:\:)\right)\cos \:\left(x\right)-\cos \:\left(90^(\circ \:\:)\right)\sin \:\left(x\right)`

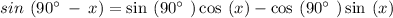
as sin 90° = 1

so sin 90° cos x = cos x

also

cos 90° = 0

so con (90°) sin x = 0

Thus, the expression becomes

`\sin \:\left(90^(\circ \:\:)\right)\cos \:\left(x\right)-\cos \:\left(90^(\circ \:\:)\right)\sin \:\left(x\right)=\cos \:\left(x\right)-0`

`= cos (x)` ∵
`\cos \left(x\right)-0=\cos \left(x\right)`

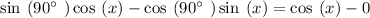
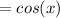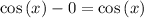
Therefore,

`\sin \left(90^(\circ \:)-x\right)=\cos \left(x\right)`

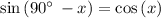
Hence, option D is correct.