Question

Two footballs (A & B) are thrown with the same amount of force. Football A has a greater mass. Describe the acceleration for each football.

Answer 1

Newton's second law gives the relationship between force applied to an object, its mass and its acceleration:

`F=ma`
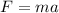
where F is the force, m the mass and a the acceleration.

A force F is applied to football A, whose mass is
`m_A`, and so the acceleration of this football will be given by (re-arranging the previous equation)

`a_A = (F)/(m_A)`

Similarly, the acceleration of football B will be

`a_B= (F)/(m_B)`
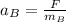
where
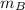
`m_B` is the mass of football B, and where the force F applied to the two footballs is the same.

Since football A has greater mass than football B,
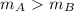
`m_A \ \textgreater \ m_B`, if we compare the two previous formula we see that the acceleration of football B is greater than the acceleration of football A:

`a_B \ \textgreater \ a_A`
Therefore, if the same force is applied to the two footballs, football B will accelerate more than football A.