Question

PLEASE HELP ME!!!!!! The transportation department of Fredrick Inc. wanted to know the mode of transport used by their employees to commute to work. The survey was conducted by randomly asking 150 employees on a day when the factory had an attendance of 1,526 employees. The survey reported that 56% of those surveyed used public transportation to commute to work. Assuming a 95% confidence level, which of the following statements holds true?

A.As the sample size is appropriately large, the margin of error is ±0.079.

B.As the sample size is too small, the margin of error is ±0.079.

C.As the sample size is appropriately large, the margin of error is ±0.094.

D.As the sample size is too small, the margin of error cannot be trusted.

Answer 1

A.

Step-by-step explanation: This is correct on edmentum/plato

Answer 2

The sample size is 150. If the sample size is greater than 30 we consider it an appropriate large sample size and can consider the population to be normally distributed. Since sample size is quite larger than 150, we assume that the sample is from the population which is normally distributed.

We are given the sample proportion p = 0.56

Sample Size = n = 150

We have to construct 95% confidence interval about the sample proportion. The z value corresponding to 95% confidence interval is 1.96. The formula to calculate the margin of error (E) is:

E= ±
`z\sqrt{(p(1-p))/(n)}`

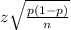
Using the values in the above formula, we get:

E =±
`1.96\sqrt{(0.56(1-0.56))/(150)}`

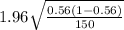
E = ± 0.079

Therefore, the correct option is:

A. As the sample size is appropriately large, the margin of error is ±0.079.