Question

What is the wavelength of a photon whose energy is twice that of a photon with a 622 nm wavelength?

Answer 1

The frequency of the
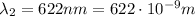
`\lambda_2 = 622 nm = 622 \cdot 10^(-9) m` wavelength photon is given by

`f_2 = (c)/(\lambda_2)= (3 \cdot 10^8 m/s)/(622 \cdot 10^(-9) m)=4.82 \cdot 10^(14) Hz`
where c is the speed of light.

The energy of this photon is

`E_2=hf_2 = (6.6 \cdot 10^(-34)Js)(4.82 \cdot 10^(14)Hz)=3.18 \cdot 10^(-19) J`
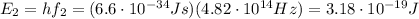
where h is the Planck constant.

The energy of the first photon is twice that of the second photon, so

`E_1 = 2 E_2 = 2 \cdot 3.18 \cdot 10^(-19)J =6.36 \cdot 10^(-19) J`

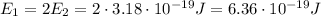
And so now by using again the relationship betwen energy and frequency, we can find the frequency of the first photon:

`f_1 = (E_1)/(h)= (6.36 \cdot 10^(-19) J)/(6.6 \cdot 10^(-34)Js)=9.64 \cdot 10^(14)Hz`

and its wavelength is

`\lambda_1 = (c)/(f_1)= (3 \cdot 10^8 m/s)/(9.64 \cdot 10^(14)Hz) =3.11 \cdot 10^(-7)m = 311 nm`
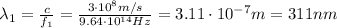
So, we see that the wavelength of the first photon is exactly half of the wavelength of the second photon (622 nm).