Question

If y varies inversely as the square of x, and y=7/4/ when x=1, find y when x=3

Answer 1

y varies inversely as the square of x. So we can write the relation between x and y as:


`y= (k)/( x^(2) )`

where k is a constant of proportionality. It is given that y = 7/4 when x = 1.
Using these values, we can write:


`(7)/(4)= (k)/(1) \\ \\ k= (7)/(4)`

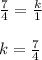
So, now the equation in terms of x and y can be written as:


`y= (7)/(4 x^(2) )`

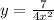
We are to find y when x = 3. So we can write:


`y= (7)/(4(9))=(7)/(36)`

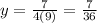Thus, for x= 3 value of y will be 7/36