The motion of the stone consists of two separate motions: in air, with average speed
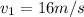
, and in the water, with average speed
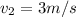
.
The total distance covered is 127 m, and it is the sum of the distances covered in air and in the water:
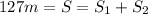
(1)
and the total time taken is the sum of the time the stone travels in air + the time the stone travels in the water:
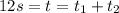
Since

, we can rewrite (1) as
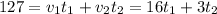
We have now a system of 2 equations with 2 unknown variables:
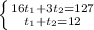
And if we solve it, we find

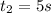
Which means that the stone travels for 7 seconds in air and for 5 seconds in the water.