Question

Even at such low fractions of the speed of light these stars are moving quite quickly (thousands of kilometers a second) compared to the standard velocity dispersion in the milky way galaxy (which is around 300km/s). suppose the star was actually moving toward the earth at a more reasonable 300km/s. what wavelength λ would the 656.46-nm line move to? use 299,792km/s for the speed of light. express your answer in nanometers to five significant figures.

Answer 1

According to Doppler Effect, an observer at rest will perceive a shift in the wavelength or frequency of the radiation emitted by a source in movement.This shift is given by the formula:

`( \lambda - \lambda_(0) )/( \lambda_(0) ) = (-v)/(c)`

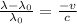
where:

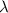
`\lambda` = observed wavelength

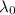
`\lambda_(0)` = wavelength at rest
v = speed of source (positive if towards the observer, negative if away from the observer)
c = speed of light

Therefore, we can solve for the observed wavelength:

`\lambda = \lambda_(0) ((-v)/(c)) + \lambda_(0) \\ \lambda = \lambda_(0) (1 - (v)/(c))`

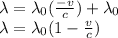
Substituting the given data:

`\lambda = 656.46 (1 - (300)/(299792))`
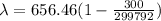
= 655.80 nm

Hence, the observed wavelength of the line would be 655.80 nm. Note that this value is smaller than the one at rest, which means that we have a blue-shift, as expected for an approaching source.