Question

Why is the graph of the rose curve r=4cos2theta

Answer 1

The correct answer is B.

Explanation:

Any point can be represented in polar form by using the notation:

`A = (r, \theta)` (1)

And any polar function must satisfy the following definition:

`r = f(\theta)`

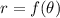
Let
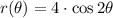`r(\theta) = 4\cdot \cos 2\theta`, where
`r` is the radial distance of any point of the curve from origin and
`\theta` is the direction of any point of the curve with respect to +x semiaxis, measured in radians.

Finally, we proceed to graph the function with the help of a graphing tool and attach the result.

Besides, we must remember that cosine is a bounded function, which means that domain and range in rectangular coordinates are represented by:

`Dom\{f\} = [-4,4]`,
`Ran\{f\} = [-4,4]`

Then, the correct answer is B.