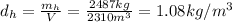Question

A hot-air balloon plus cargo has a mass of 326 kg and a volume of 2310 m3 on a day when the outside air density is 1.22 kg/m3. the balloon is floating at a constant height of 9.14 m above the ground.

Answer 1

Missing question: "what is the density of the hot air?"

Solution:

The balloon is floating at constant height, and this means that the two forces acting on it (the weight and the buoyant force) are in equilibrium:

`W=B`
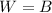
where W is the weight of the balloon, which is sum of the weight of the balloon structure and of the hot air inside the balloon, and B is the buoyant force.

The buoyant force is given by:

`B=Vd_ag`
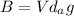
where V is the volume of the balloon, d is the air density and g is the gravitational acceleration. Plugging numbers into the equation, we find

`B=Vd_ag=(2310 m^3)(1.22 kg/m^3)(9.81 m/s^2)=2.76 \cdot 10^4 N`

This is equal to the weight of the balloon+hot air inside it:

`2.76 \cdot 10^4 N = W = W_b + W_h`
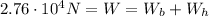
where

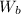
`W_b` is the weight of the balloon

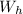
`W_h` is the weight of the hot air inside the balloon

The weight of the balloon is

`W_b = mg = (326 kg)(9.81 m/s^2)=3199 N`

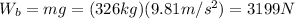
Which means that the weight of the hot air is

`W_h = W-W_b = 2.76 \cdot 10^4 N - 3199 N =2.44 \cdot 10^4 N`
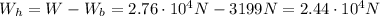
which corresponds to a mass of

`m_h = (W_h)/(g)= (2.44 \cdot 10^4 N)/(9.81 m/s^2)=2487 kg`

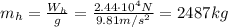
And since the mass is the product between density and volume, we can find the density of the hot air:

`d_h = (m_h)/(V)= (2487 kg)/(2310 m^3)=1.08 kg/m^3`