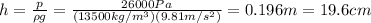Question

A beaker containing mercury is placed inside a vacuum chamber in a laboratory. the pressure at the bottom of the beaker is 26000 pa. what is the height of the mercury in the beaker? the acceleration of gravity is 9.81 m/s 2 .

Answer 1

The mercury density (at liquid state) is

`\rho = 13.5 g/cm^3=13500 kg/m^3`

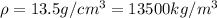
And we know that the pressure at the bottom of a column of fluid is given by (Stevin's law)

`p=\rho g h`
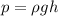
where

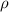
`\rho` is the liquid density
g is the gravitational acceleration
h is the height of the column of fluid

The pressure at the bottom of the beaker is
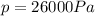
`p=26000 Pa`, therefore we can re-arrange the previous equation to get the height of the column of mercury

`h= (p)/(\rho g)= (26000 Pa)/((13500 kg/m^3)(9.81 m/s^2))=0.196m = 19.6 cm`