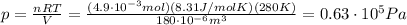Question

A canister containing air has a volume of 85 cm 3 and a pressure of 1.45 atm when the temperature is 310 k. what is the pressure when the volume is increased to 180 cm 3 and the temperature is reduced to 280 k?

Answer 1

We can solve the problem by using the ideal gas law, which states:

`pV=nRT`
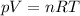
where
p is the gas pressure
V is the volume
n is the number of moles
R is the gas constant
T is the absolute temperature

The initial conditions of the gas in the problem are:

`p=1.45 atm =1.47 \cdot 10^5 Pa`

`V=85 cm^3 = 85 \cdot 10^(-6) m^3`

`T=310 K`
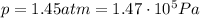
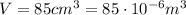
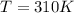
So we can use the previous equation to find the number of moles of the gas:

`n= (pV)/(RT)= ((1.47 \cdot 10^5 Pa)(85 \cdot 10^(-6) m^3))/((8.31 J/mol K)(310 K)) =4.9 \cdot 10^(-3) mol`

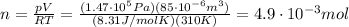
The final conditions of the gas are:

`V=180 cm^3 = 180 \cdot 10^(-6) m^3`

`T=280 K`
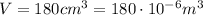
and since the number of moles didn't change, we can find the final pressure by using again the ideal gas law:

`p= (nRT)/(V)= ((4.9 \cdot 10^(-3) mol)(8.31 J/mol K)(280 K))/(180 \cdot 10^(-6) m^3)=0.63 \cdot 10^5 Pa`