Question

Worth 99 points!

Use the midpoint rule with n=4 to approximate the area of the region bounded by y=x^3 and y=x.

Must use the Midpoint Rule! Please help, thank you.

Answer 1

Area = 0.21875

Explanation:

Formula: x = b - a/n

Solve: 1 - (-1)/4 = 2/4 = 1/2 = 0.5

Subinterval: (0,1)

Midpoint 1 : f(0.5)/2 = 0.25

Midpoint 2: f(1 + 0.5)/2 = 0.75

Put in equation: (0.75 * 0.5) + (0.25 * 0.5)

Simplify: 0.5

x^3: 0.25^3 + 0.75^3 * 0.5

Answer: 0.21875

Answer 2

The objective is to find total bounded area. Intersections occur at x=-1, x=0, and x=1. Since we need 4 subintervals, we split the line segment from -1 to 1 into four line segment.

That would be
`\Delta x = (b-a)/(n) = (1 - \text-1)/(4) = \frac12`

So subintervals would be
[-1, -0.5]
[-0.5, 0]
[0, 0.5]
[0.5, 1]

Since segment was split evenly, because of rotate symmetry, sub-area for [-1,0] and [0,1] would be same so we can just focus on interval [0,1] with n=2 and then multiple the result by 2.

Now we are talking about midpoint rules, the height of rectangle for [0,0.5], [0.5,1] would be
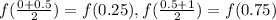
`f(\frac{0+0.5}2)=f(0.25), f(\frac{0.5+1}2)=f(0.75)` respectively. Width of rectangle would be
`\Delta x = 0.5`.

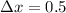
Hence for
`x`, that would be

`f(0.25)\Delta x + f(0.75)\Delta x = 0.25\cdot0.5 + 0.75\cdot0.5 = 0.5`

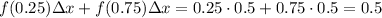
And
`x^3` would be

`(0.25)^3\cdot0.5+(0.75)^3\cdot0.5 = 0.21875`

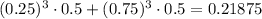
So the approximate area is 0.28125.

Now double that to account for area from [-1,0] and our answer is 0.5625.

Is this clear?