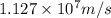Answer: The velocity of released alpha particle is
Step-by-step explanation:
According to law of conservation of momentum, momentum can neither be created nor be destroyed until and unless, an external force is applied.
For a system:
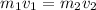
where,
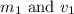 = Initial mass and velocity
= Initial mass and velocity
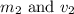 = Final mass and velocity
= Final mass and velocity
We are given:
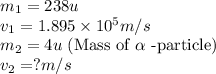
Putting values in above equation, we get:
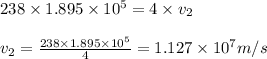
Hence, the velocity of released alpha particle is