Question

Please help me with 21 and 22! Thank you.

Answer 1

#21

To find the area of rectangle, you multiple length by width, so that would be
`(\ √(2x)\ )(\ √(6x)\ ) = √(2x\cdot6x) = √(12x^2) = x√(4\cdot3) = \boxed{2x\sqrt3}`

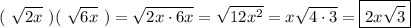
Since we are talking about area \ length, x need to be positive so we don't need to worry about absolute value now.

#22

The area of triangle is
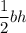
`\frac12bh`, so that would be

`\frac12√(18y)\cdot√(2y^4)\\\ \\=\frac{y^2}2√(18y)\cdot√(2)\\\ \\=\frac{y^2}2√(18y\cdot2)\\\ \\=\frac{y^2}2√(36y)\\\ \\=\frac{y^2}2√(4\cdot9\cdot y)\\\ \\=\boxed{3y^2\sqrt y}\text{ or }\boxed{3√(y^5)}`

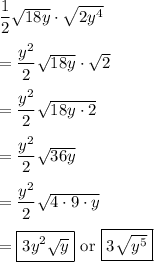
Hope this helps.