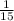Question

Mrs. Jones buys two toys for her son. The probability that the first toy is defective is 1/3, and the probability that the second toy is defective given that the first toy is defective is 1/5. What is the probability that both toys are defective?

Answer 1

Answer:
`(1)/(15)`

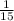
Explanation:

Let F denote the event of first toy is defective and S denote the second toy is defective .

Given: The probability that the first toy is defective
`P(F)=(1)/(3)`

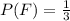
The probability that the second toy is defective given that the first toy is defective
`P(S|F)=(1)/(5)`

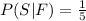
The formula to calculate the conditional probability is given by :-

`P(S|F)=(P(S\cap F))/(P(F))\\\\\Rightarrow P(S\cap F)=P(S|F)* P(F)\\\\\Rightarrow\ P(S\cap F)=(1)/(3)* (1)/(5)=(1)/(15)`

Hence, the probability that both toys are defective=
`(1)/(15)`

Answer 2

Probability=
`(1)/(15)`

Explanation:

As it is given that

Probability of toy A is defective is =P(A) =
`(1)/(3)`

Probability of toy b is defective if A is defective = P (B)=
`(1)/(5)`

WE have to find the P(A n B)

By the law of Probability

P(A n B) = P (A).P(B)

putting the values given to us

P(AnB)=
`(1)/(3)` *
`(1)/(5)`

Probability=
`(1)/(15)`