Question

Eric leans a ladder against the roof of his house so that the ladder forms a 2004-04-02-01-00_files/i0260000.jpg angle with the ground. The roof of the house is 13 feet above the ground. How far is the bottom of the ladder from the base of the house? Round the answer to the nearest tenth.

Answer 1

A right angled triangle can be formed from the given scenario as shown below in the figure:

We have a perpendicular(opposite side), the measure of angle and we are interested in finding the hypotenuse.

sine of the angle relates its perpendicular side to hypotenuse as:

sin(x) = perpendicular/hypotenuse

⇒

Hypotenuse = Perpendicular/sin(x) = 13/sin(70) = 13.8 feet

This means, the length of the ladder is 13.8 feet, rounded to nearest tenth.

Answer 2

4.7 ft.

Explanation:

Let x represent the distance of the bottom of the ladder from the base of the house.

We have been given that Eric leans a ladder against the roof of his house so that the ladder forms a 70 angle with the ground. The roof of the house is 13 feet above the ground.

Upon looking at our attached graph we can see that ladder and wall of house forms a right triangle with respect to ground, where x is adjacent and side with 13 ft length is opposite side to the angle of 70 degrees.

We know that tangent relates opposite side of a right triangle with adjacent, so we can set an equation as:

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(70^(\circ))=(13)/(x)`

`x=\frac{13}{\text{tan}(70^(\circ))}`

`x=(13)/(2.747477419455)`

`x=4.7316\approx 4.7`

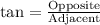
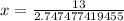
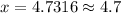
Therefore, the bottom of ladder is 4.7 feet away from the base of the house.