A quadratic function is a function of the form
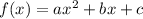
. The
vertex,
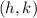
of a quadratic function is determined by the formula:

and
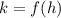
; where

is the
x-coordinate of the vertex and

is the
y-coordinate of the vertex. The value of

determines if the
parabola opens upward or downward; if
 is positive, the parabola opens upward and the vertex is the minimum value, but if
is positive, the parabola opens upward and the vertex is the minimum value, but if
 is negative the graph opens downward and the vertex is the maximum value. Since the quadratic function only has one vertex, it could not contain both a minimum vertex and a maximum vertex at the same time.
is negative the graph opens downward and the vertex is the maximum value. Since the quadratic function only has one vertex, it could not contain both a minimum vertex and a maximum vertex at the same time.