Remember that the velocity as a function of time is the derivative of the position as a function of time.
To solve this we are going to take the derivative of our position function
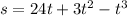
. To do that er are going to apply the power rule of calculus:
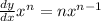
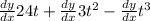
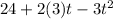
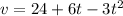
We can conclude that the correct answer is:
B. V = 24 + 6t - 3t2