Question

What is the y-intercept of the quadratic function fx) (x- 6)(x-2)?

Answer 1

The answer is B just took the test

Explanation:

Answer 2

Option 1
To find the y-intercept of a quadratic that is in factor formed follow the steps below:

First take the factor form and put it into standard quadratic form
Standard quadratic form:

`ax^2 + bx + c`

To put the the factor form of a qudratic into standard form, we use the foil method

(x-6)(x-2) =
`x^2 - 8x +12`

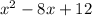
Now to find the y-intercept, input 0 where the x is located:


`f(x) = x^2 - 8x +12`

`f(0) = 0^2 - 8(0) +12`

`f(0) = 12`
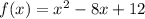
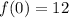
y-intercept = (0,12)

Why did I use 0? Remember the y-intercept is where the line crosses the y axis so this means the x value of the y intercept is always = 0. Also, not, to find the y-intercept, you could of just multiplied the 6 and 2 in the factored form to get the 12 and since you know that the x is always 0 at the y-intercept, you know that the y-intercept is at (0,12)

Option 2
Input 0 for x in f(x) = (x-6)(x-2)
f(x) = (x-6)(x-2)
f(0) = (0 - 6)(0 - 2)
f(0) = (6)(2) = 12
x = 0
f(0) = y = 12
y-intercept = (0,12)