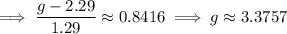The smallest GPA needed to fall in the top 20% is
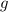
, where
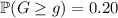
where
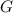
is a random variable denoting GPA scores. Transform
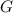
to the standard normal random variable
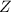
using
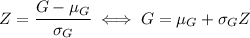
where
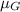
and
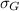
are the mean and standard deviation of
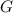
, respectively. Now
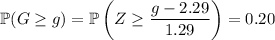
Using the inverse CDF for the standard normal distribution, we find that the corresponding critical value is about 0.8416, which means