Question

Each hexagon tile has an area of LaTeX: 18\sqrt{3} 18 3 in.2 . Solve for x. Then find the exact length of each side of the hexagon. (Hint: Six equilateral triangles make one hexagon.)

Answer 1

The length of the side of the hexagon is
`2√(3)` inches.

Explanation:

According to this question, we have a regular hexagon with a surface area of
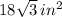`18√(3)\,in^(2)`. From Geometry, we know that all regular hexagons can be formed by six regular triangles, since the angle of one complete revolution (360º) divided by the number of triangles is equal to the internal angle of each triangle (60º). Then, the area of each triangle is found after dividing the complete area by the number of regular triangles:

`A_(\triangle) = (18√(3)\,in^(2))/(6)`

`A_(\triangle) = 3√(3)\,in^(2)`

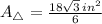
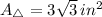
The area of the triangle as a function of the length of the side of the hexagon (
`l`), measured in inches, is determined by this equation:

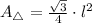`A_(\triangle) = (√(3))/(4) \cdot l^(2)` (1)

If we know that
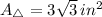`A_(\triangle) = 3√(3)\,in^(2)`, then the length of the side of the hexagon is:

`(4)/(√(3))\cdot A_(\triangle) = l^(2)`

`l^(2) = (4\cdot √(3))/(3) \cdot A_(\triangle)`

`l = 2\sqrt{(√(3))/(3)\cdot A_(\triangle) }`

`l = 2√(3)\,in`

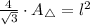
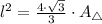
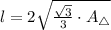
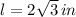
The length of the side of the hexagon is
`2√(3)` inches.