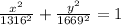Question

A satellite is to be put into an elliptical orbit around a moon. A vertical ellipse is shown surrounding a spherical object labeled moon The moon is a sphere with radius of 959 km. Determine an equation for the ellipse if the distance of the satellite from the surface of the moon varies from 357 km to 710 km.

Answer 1

The answer is (x^2 / 1316^2) + (y^2 / 1669^2) = 1

Answer 2

The equation of the ellipse is :

`(x^2)/(1316^2)+(y^2)/(1669^2)=1`

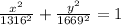
Explanation:

Formula for the equation of an ellipse is given by :

`(x^2)/(a^2)+(y^2)/(b^2)=1`

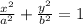
where a and b are the horizontal and vertical intercepts of the ellipse on the coordinate axis.

Here, a = 959 + 357

= 1316

And, b = 959 + 710

= 1669

So, the equation of the ellipse is :

`(x^2)/(1316^2)+(y^2)/(1669^2)=1`