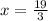Question

PLEASE HELP!! What is the value of x?

Answer 1

To find x, first we'll split the triangle in two right triangles.

The first triangle will be the one with sides (8,x+4,y) and the second triangle will be the one with sides (12,2x+1,y).

As you can see, these two triangles share the side 'y'.

To solve we'll do the following; first solve for 'y' by applying the Pythagorean theorem in the second triangle, and finally solve for 'x' applying Pythagorean theorem in the first triangle.

From the second triangle (12,2x+1,y) we solve for 'y' by writing:

`y^(2)=12^(2)- (2x+1)^(2)=144-4 x^(2) -4x-1=`

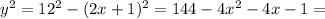
Now that we know 'y^2' we apply Pythagorean Theorem in the first triangle (8,x+4,y)

`8^(2)= (x+4)^(2)+ y^(2)= (x^(2)+8x+16)+(143-4 x^(2) -4x)`

`64=159-3 x^(2) +4x`

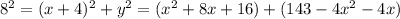
Now you solve the quadratic equation, you'll get a positive and negative value; as this are lengths, you take the positive and get:


`x= (19)/(3)`