Question

Anna has leaned a ladder against the side of her house. The ladder forms a 72º angle with the ground and rests against the house at a spot that is 6 meters high. What length is the best approximation for the distance along the ground from the bottom of the ladder to the wall?

Answer 1

The answer is 2 m hope this helps

Answer 2

The best approximation of AB is 2 meters.

Explanation:

Notice that this situation models a right triangle, when the height, which is a leg of the triangle, is 6 meters.

Also, we know the angle between the ladder and the ground, which is 72°.

To find the distance from A to B, which from the bottom of the ladder to the bottom of the wall, we just need to use trigonometric reasons.

`tan(72\°)=(opposite \ leg)/(adjacent \ leg)`

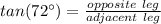
Why we use tangent? Because it relates both legs where we just need to find the adjacent one.

`tan(72\°)=(6)/(AB)\\AB=(6)/(tan(72\°)) \\AB \approx (6)/(3) \\AB \approx 2 \ m`

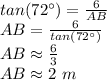
Therefore, the best approximation of AB is 2 meters.