Question

Peter decides to invest $1,200,000 in a period annuity that earns 4.6% APR compounded monthly for a period of 20 years. How much money will Peter be paid each month?

Answer 1

Given is the Present Value of annuity, PV = 1,200,000 dollars.

Given that 4.6% APR compounded monthly i.e. r = 4.6%/12 = 0.003833

Given that 20 years of investment i.e. N = 20x12 = 240

It says to find monthly income from the annuity.

We know the formula for Periodic Payment (when PV is known) is given as follows :-

`Periodic \;payment = (PV)/((1-(1)/((1+r)^(N)))/(r)) \\\\Periodic \;payment = (1,200,000)/((1-(1)/((1+0.003833)^(240)))/(0.003833)) \\\\Periodic \;payment = (1,200,000)/((1-(1)/((1.003833)^(240)))/(0.003833)) \\\\Periodic \;payment = (1,200,000)/((1-(1)/(2.504681211))/(0.003833)) \\\\Periodic \;payment = (1,200,000)/((1-0.399252406)/(0.003833)) \\\\Periodic \;payment = (1,200,000)/((0.600747594)/(0.003833))`

`Periodic \;payment = (1,200,000)/(156.7303924) \\\\Periodic \;payment = 7656.460128 \\\\Periodic \;payment = 7656.46 \;dollars \;per \;month`

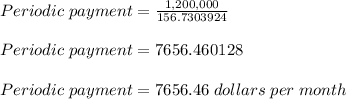
Hence, Monthly Income would be 7,656.46 dollars.