Question

Which expression is equivalent to 4 sqrt 16x^11y^8/81x^7y^6

Answer 1

The given expression 4 sqrt(16x^11y^8/81x^7y^6) simplifies to (4/9) * x^2 * y by taking the square root of each term separately and then simplifying the powers of x and y.

Step-by-step explanation:

The expression given is 4 sqrt(16x^11y^8/81x^7y^6). To simplify this expression, we need to apply the square root to both the numerator and the denominator separately and simplify any like terms, as well as using the property of exponents to simplify the powers of x and y.

We start by simplifying the square root of each component:

• Square root of 16 is 4.
• x^11 under the square root becomes x^(11/2).
• Similarly, y^8 under the square root becomes y^(8/2), which is y^4.
• The square root of 81 is 9.
• x^7 under the square root becomes x^(7/2).
• y^6 under the square root becomes y^(6/2), which is y^3.

Now, divide and simplify:

(4 * x^(11/2) * y^4) / (9 * x^(7/2) * y^3) = (4/9) * x^((11/2) - (7/2)) * y^(4 - 3)

Therefore, we get:

(4/9) * x^2 * y

Answer 2

The first step for finding out whether or not this expression is equivalent to
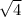
`√(4)` is to reduce the fraction with
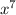
`x^(7)`. You can begin to do this by dividing the terms with the same base by subtracting their exponents.

`(16 x^(11-7) y^(8) )/(81 y^(6) )`
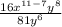
Subtract the exponents.

`(16 x^(4) y^(8) )/(81 y^(6) )`
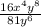
Now reduce the fraction with
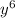
`y^(6)` by doing the same process. Since I just showed you how to do this,, I will skip over this.

`(16 x^(4) y^(2) )/(81)`
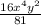
Since we cannot simplify this expression any further,, your answer is going to be
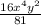
`(16 x^(4) y^(2) )/(81)`,, which is not equivalent to
`√(4)`.
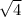
Let me know if you have any further questions.
:)