Derivative, by first principle \tan( √(x ) )

Question

Derivative, by first principle

`\tan( √(x ) )`

Answer 1

`\displaystyle\lim_(h\to0)\frac{\tan√(x+h)-\tan x}h`

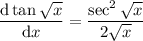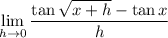
Employ a standard trick used in proving the chain rule:


`(\tan√(x+h)-\tan x)/(√(x+h)-\sqrt x)\cdot\frac{√(x+h)-\sqrt x}h`

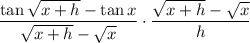
The limit of a product is the product of limits, i.e. we can write


`\displaystyle\left(\lim_(h\to0)(\tan√(x+h)-\tan x)/(√(x+h)-\sqrt x)\right)\cdot\left(\lim_(h\to0)\frac{√(x+h)-\sqrt x}h\right)`

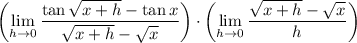
The rightmost limit is an exercise in differentiating
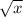
`\sqrt x` using the definition, which you probably already know is
`\frac1{2\sqrt x}`.

For the leftmost limit, we make a substitution
`y=\sqrt x`. Now, if we make a slight change to
`x` by adding a small number
`h`, this propagates a similar small change in
`y` that we'll call
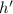
`h'`, so that we can set
`y+h'=√(x+h)`. Then as
`h\to0`, we see that it's also the case that
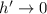
`h'\to0` (since we fix
`y=\sqrt x`). So we can write the remaining limit as


`\displaystyle\lim_(h\to0)(\tan√(x+h)-\tan\sqrt x)/(√(x+h)-\sqrt x)=\lim_(h'\to0)(\tan(y+h')-\tan y)/(y+h'-y)=\lim_(h'\to0)(\tan(y+h')-\tan y)/(h')`

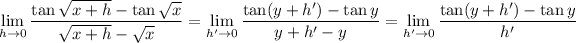
which in turn is the derivative of
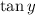
`\tan y`, another limit you probably already know how to compute. We'd end up with
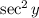
`\sec^2y`, or
`\sec^2\sqrt x`.

So we find that


`(\mathrm d\tan\sqrt x)/(\mathrm dx)=(\sec^2\sqrt x)/(2\sqrt x)`