Answer:
The measure of the larger is
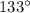 .
.
Explanation:
Given:
The measure of an angle is
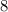 degrees less than three times the measure of another angle.
degrees less than three times the measure of another angle.
The two angles are supplementary.
To find: The measure of the larger angle.
Solution:
Let the measure of the smaller angle be
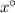 .
.
Then the measure of the larger angle be
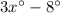 .
.
The two angles are supplementary, so their sum is
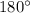 .
.
So,

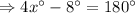
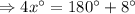
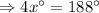
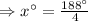
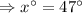
So, the measure of the smaller angle is
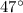 .
.
And, the measure of the larger angle is
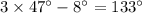 .
.
Hence, the measure of the larger is
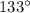 .
.