Answer: c.the set of all integers, the set of all rational numbers, and the set of all real numbers
Explanation:
The given number is
 .
.
We know that
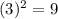 and
and
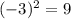
Therefore,
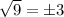
Therefore, the value of
 does not belongs to the set of natural numbers since -3 does not belongs to it.
does not belongs to the set of natural numbers since -3 does not belongs to it.
Since 3,-3 belongs to the set of integers.
Thus, the value of
 belongs to the set of integers the set of all rational numbers, and the set of all real numbers because the set of integers is contained in the set of rationals and the set of rational is contained in the set of real numbers.
belongs to the set of integers the set of all rational numbers, and the set of all real numbers because the set of integers is contained in the set of rationals and the set of rational is contained in the set of real numbers.