Question

In the equation f(x) = (3x + 5) (x2 - 6x + 9)2 = 0, 3 has a multiplicity of ______.

Answer 1

multiplicity is how many times the root (or zero) is repeated

example, in
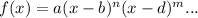
`f(x)=a(x-b)^n(x-d)^m...` the root b has a multiplicity of n and the root d has a multiplicity of m

first we need to get the roots into
`f(x)=a(x-b)^n(x-d)^m`
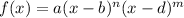
for (3x+5), we need to force factor out the 3 to get

`3(x+\frac{5/3})`

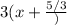
factor the other one

`(x^2-6x+9)=(x-3)(x-3)=(x-3)^2`
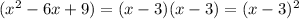
but it is
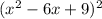
`(x^2-6x+9)^2` which is equivilent to
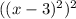
`((x-3)^2)^2` which simplifies to
`(x-3)^4`

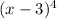
so we get

`f(x)=3(x+(5)/(3))(x-3)^4`
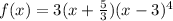
so the roots are -5/3 multiplicity 1 and 3 multiplicity 4


3 has a multilicity of 4