Question

The sum of first three terms of a finite geometric series is -7/10 and their product is -1/125. [Hint: Use a/r, a, and ar to represent the first three terms, respectively.] The three number are __, __, and __

Answer 1

2r²-5r+2=0

a=2

b=-5

c=2

Explanation:

Answer 2

ooh, fun

geometric sequences can be represented as

`a_n=a(r)^(n-1)`
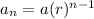
so the first 3 terms are

`a_1=a`

`a_2=a(r)`

`a_2=a(r)^2`

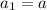
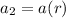
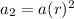
the sum is -7/10

`(-7)/(10)=a+ar+ar^2`
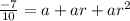
and their product is -1/125

`(-1)/(125)=(a)(ar)(ar^2)=a^3r^3=(ar)^3`

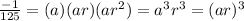
from the 2nd equation we can take the cube root of both sides to get

`(-1)/(5)=ar`
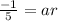
note that a=ar/r and ar²=(ar)r
so now rewrite 1st equation as

`(-7)/(10)=(ar)/(r)+ar+(ar)r`
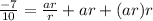
subsituting -1/5 for ar

`(-7)/(10)=((-1)/(5))/(r)+(-1)/(5)+((-1)/(5))r`
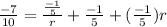
which simplifies to

`(-7)/(10)=(-1)/(5r)+(-1)/(5)+(-r)/(5)`
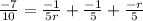
multiply both sides by 10r
-7r=-2-2r-2r²
add (2r²+2r+2) to both sides
2r²-5r+2=0
solve using quadratic formula
for
`ax^2+bx+c=0`

`x=(-b \pm √(b^2-4ac))/(2a)`
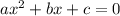
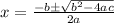
so
for 2r²-5r+2=0
a=2
b=-5
c=2


`r=(-(-5) \pm √((-5)^2-4(2)(2)))/(2(2))`

`r=(5 \pm √(25-16))/(4)`

`r=(5 \pm √(9))/(4)`

`r=(5 \pm 3)/(4)`
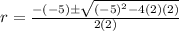
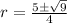
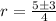
so

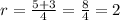
`r=(5+3)/(4)=(8)/(4)=2` or
`r=(5-3)/(4)=(2)/(4)=(1)/(2)`

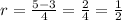
use them to solve for the value of a

`(-1)/(5)=ar`

`(-1)/(5r)=a`
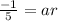
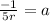
try for r=2 and 1/2

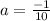
`a=(-1)/(10)` or
`a=(-2)/(5)`


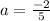
test each
for a=-1/10 and r=2
a+ar+ar²=
`(-1)/(10)+(-2)/(10)+(-4)/(10)=(-7)/(10)`
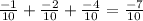
it works

for a=-2/5 and r=1/2
a+ar+ar²=
`(-2)/(5)+(-1)/(5)+(-1)/(10)=(-7)/(10)`
it works


both have the same terms but one is simplified

the 3 numbers are
`(-2)/(5)`,
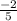
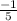
`(-1)/(5)`, and
`(-1)/(10)`