Question

To solve this system of equations by elimination, what operation could be used to eliminate the y-variable and find the value of x? 2x − 4y = 6 −3x + 3y = 12 A) add 3 times the second equation to 4 times the first equation B) add 4 times the second equation to 3 times the first equation C) subtract 3 times the second equation from 4 times the first equation D) subtract 4 times the second equation from 3 times the first equation

Answer 1

Option B

Explanation:

Given is a system of two equations as

`2x − 4y = 6 \\−3x + 3y = 12`

To solve them using elimination:

Elimination method is the method of making coefficients of one variable numerically equal

IN the given system we have -4 as coefficient for y in I equation and 3 for y in II equation.

To make them numerically equal with opposite signs we can multiply I equation by 3 and II by 4

WE get

`6x-12y =18\\-12x+12y=48`

Now if we add these two we are able to eliminate y from the system

Adding gives

`-6x=66\\x=-11`

So option B is right

Answer 2

Option B is correct.

add 4 times the second equation to 3 times the first equation

Explanation:

Given the system of equation:

`2x - 4y = 6` ......[1]

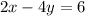`-3x + 3y =12` .....[2]

Multiply equation [1] by 3 we get;

`3(2x-4y) = 3 \cdot 6`

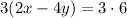
Using distributive property;
`a\cdot (b+c) = a\cdot b+ a\cdot c`

6x - 12y = 18 .......[3]

Multiply equation [2] by 4 we get;

`4(-3x+3y) = 4 \cdot 12`

Using distributive property we get;

-12x + 12y = 48 ......[4]

Add equation [3] and [4] to eliminate y and solve for x;

(6x -12y) + ( -12x +12y ) = 18 + 48

6x - 12y -12x + 12y = 66

Combine like terms;

6x - 12x = 66

or

-6x = 66

Simplify:

x = -11

Therefore, the operation which could be used to eliminate the y-variable and find the value of x is;

add 4 times the second equation to 3 times the first equation.