Answer:
The standard deviation rounded to the nearest hundredth is 10.02.
Explanation:
The formula to find the standard deviation is
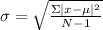
Where
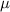 represents the mean,
represents the mean,
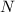 the total number of elements and
the total number of elements and
 is each element.
is each element.
So, first we need to find the mean
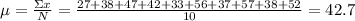
Then, we subtract the mean with each element and find its square power
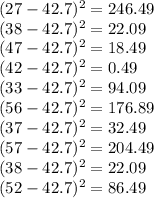
Then, we sum all, and that would be the numerator to find the standard deviation
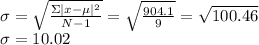
Therefore, the standard deviation rounded to the nearest hundredth is 10.02.