Question

Find the equation for the plane through the points upper p 0 left parenthesis negative 2 comma negative 5 comma negative 4 right parenthesis​, upper q 0 left parenthesis 5 comma 1 comma negative 4 right parenthesis​, and upper r 0 left parenthesis negative 1 comma 2 comma 5 right parenthesis.

Answer 1

We can suppose the equation of the plane is in the form ...
ax +by +cz = 1
By using the given point coordinates for x, y, and z, we end up with three equations in 3 unknowns. These can be described by the augmented matrix ...

`\left[\begin{array}ccc-2&-5&-4&1\\5&1&-4&1\\-1&2&5&1 \end{array}\right]`
Putting this in reduced row-echelon form, we find
a = 54/35
b = -63/35
c = 43/35

The equation of the plane through
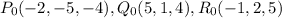
`P_(0)(-2,-5,-4), Q_(0)(5,1,4), R_(0)(-1,2,5)` is ...
54x -63y +43z = 35