Given:
The parent absolute function is
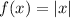
To find:
The new function if the parent function is translated up by 5 units and vertically stretched by a factor of 3.
Solution:
The translation is defined as
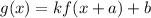 .... (1)
.... (1)
Where, k is stretch factor, a is horizontal shift and b is vertical shift.
If 0<k<1, then the graph compressed vertically by factor k and if k>1, then the graph stretch vertically by factor k.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.
Parent function is translated up by 5 units. So, b=5
It is vertically stretched by a factor of 3. So, k=3.
There is no horizontal shift. So, a=0.
Now, putting k=3, a=0 and b=5 in (1), we get
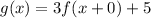

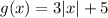
![[\because f(x)=|x|]](https://img.qammunity.org/2022/formulas/mathematics/high-school/s13gya4ifi5eva2ye1hz19zhdsaaovjbn6.png)
Therefore, the correct option is D.