Question

Please solve both and tell me how!

Answer 1

PART A:
To determine k, you need to throw x + 3 into the original function:


`f(x)= x^(2) -2x-24`

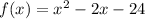
So,
`f(x+3)` would be:


`f(x+3)= (x+3)^(2) -2(x+3)-24`

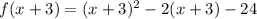
Doing some FOILing/distributing, we get:


`f(x+3)= (x^(2)+6x+9) -2x-6-24`

Doing some clean up/combining like terms, we get:


`f(x+3)= x^(2)+4x-21`

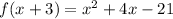
Now, it should be clear that k=4, since k is the coefficient in front of the x term (it's the "b" in
`ax^2+bx+c`).

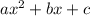
PART B:
There are several ways to find the zeros, but perhaps the easiest is to factor the result from Part A:


`f(x+3)= x^(2)+4x-21=(x+7)(x-3)`

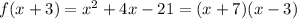
From those factors, we know that zeros occur at x = -7 and x = 3 (answers A and E).

By the way, you can check the logic of these zeros if you know about shifts/translations.
`f(x+3)` is a 3 unit left shift from the original function, which has zeros at x = -4 and x = 6. Well, x = -7 is 3 units to the left of x = -4. And x = 3 is 3 units to the left of x = 6. So everything seems to check out.