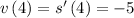Answer:
Instantaneous Velocity is
Explanation:
Velocity refers to the speed along with direction or we can say velocity refers to rate of change of position of an object with respect to time.
Let
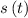 be the position of object . Then the instantaneous velocity is given by
be the position of object . Then the instantaneous velocity is given by
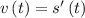 . At time
. At time
 , velocity is given by
, velocity is given by

Given:
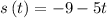
On differentiating with respect to time t , we get :
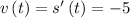
At
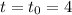 ,
,